Next Permutation Algorithm

June 12, 2021

Python, as of v3.9.5, doesn’t have the equivalent of the C++ function std::next_permutation. This function rearranges elements into the next lexicographically greater permutation.

There is a permutation function in the itertools library, but it generates a permutation, not in lexicographic order. For example:

from itertools import permutation
# next permutation should be [3,1,2]
arr = [2,3,1]

p = permutation(arr)

# first result returns the input array (unchanged)
next(p) # (2, 3, 1)
next(p) # (2, 1, 3) NOT lexicographically greater
next(p) # (3, 2, 1) NOT lexicographically greater
next(p) # (3, 1, 2) correct answer

Lexicographic Ordering

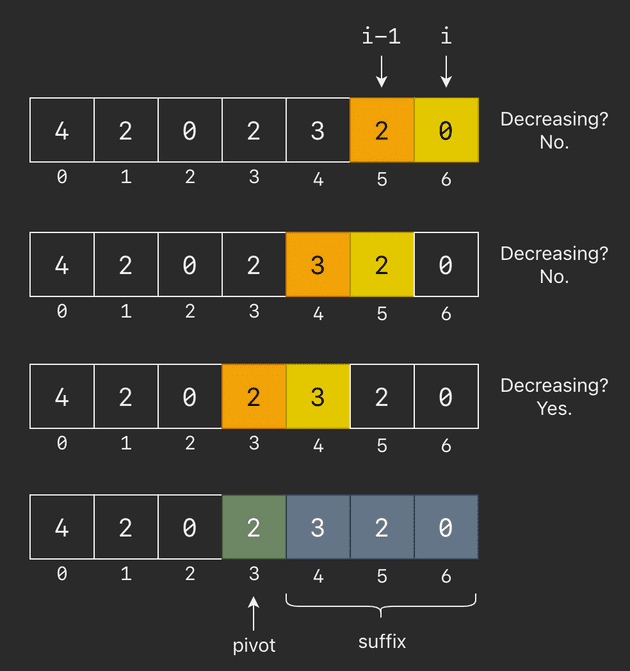
Iterating from right to left, there will be a point when the elements start decreasing (i.e. the value at index i-1 is less). We’ll call this the pivot, and the portion from pivot to the right end the suffix.

pivot = 0

# iterate right-to-left
# Note: for loop stops one index before 0
for i in range(len(nums)-1, 0, -1):
    # check if next element is decreasing
    if nums[i-1] < nums[i]:
        pivot = i-1
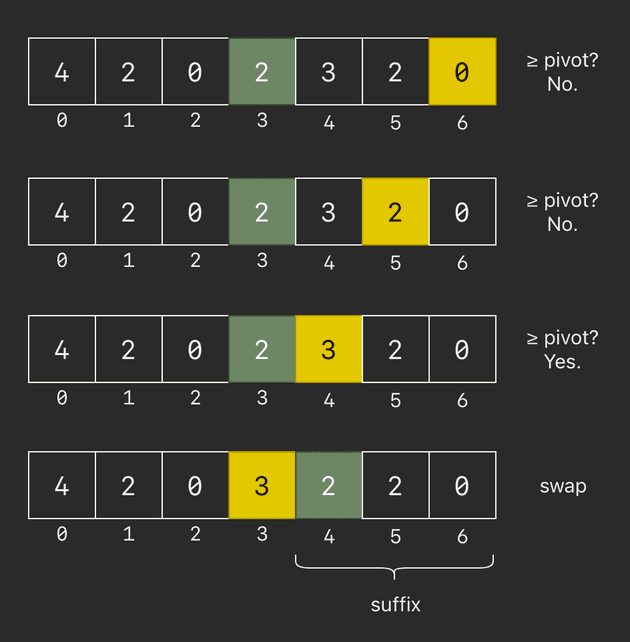
        break

In the suffix, iterate from right to left (again), looking for the smallest value greater than or equal to the pivot. This value will be swapped with pivot.

# right-to-left, but stop before pivot
for j in range(len(nums)-1, pivot, -1):
    # swap if some number in suffix
    # is greater than pivot
    if nums[j] > nums[pivot]:
        nums[j], nums[pivot] = nums[pivot], nums[j]
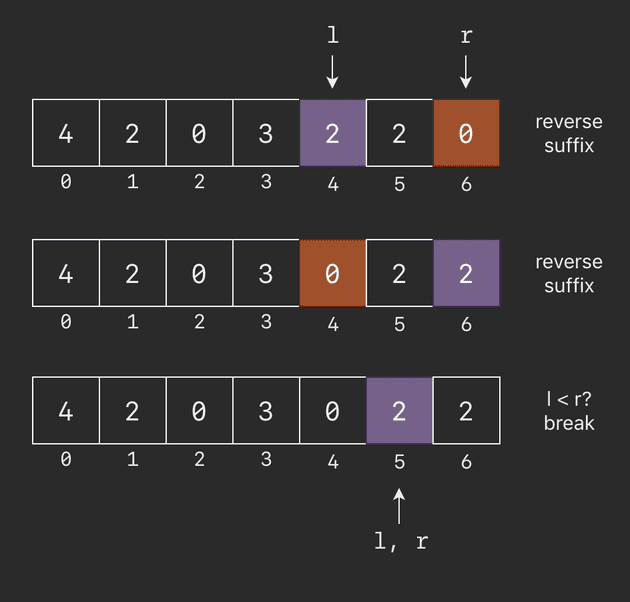
        break

After swapping, the final thing left to do is reversing the suffix portion. We can do this in-place using two pointers and swapping.

l = pivot+1     # suffix start
r = len(nums)-1 # suffix end (always rightmost)

while l < r:
    nums[l], nums[r] = nums[r], nums[l]
    l += 1
    r -= 1

And the result will be the next lexicographically greater permutation. Below is the complete code:

def nextPermutation(nums):
    
    pivot = 0
    
    for i in range(len(nums)-1, 0, -1):
        if nums[i-1] < nums[i]:
            pivot = i-1
            break
    else:
        nums.sort()
        return nums
    
    for j in range(len(nums)-1, pivot, -1):
        if nums[j] > nums[pivot]:
            nums[j], nums[pivot] = nums[pivot], nums[j]
            break
    
    l = pivot+1
    r = len(nums)-1
    
    while l < r:
        
        nums[l], nums[r] = nums[r], nums[l]
        
        l += 1
        r -= 1
    
    return nums